論文読み「Mipmapping Normal Maps」

2004 年あたりのホワイトペーパーの「Mipmapping Normal Maps」を流し読みしたので、雑に覚書のメモを書いておきます。 paper の著者は Michael Toksvig という方です。

断りが無い限り、図表は paper からの引用です。

何をやっているか

Mipmap というのは、テクスチャを遠くに配置したときに、近くのテクスチャをそのまま使うとモアレが発生したりジャギーが発生したりするので、あらかじめテクスチャを縮小したものを複数用意しておき、距離に応じて適切な解像度のテクスチャを使うという技術です。

法線マップについても同様に mipmap を用意する必要がありますが、法線マップの場合は色の mipmap を作るみたいに単純にテクスチャを縮小して周囲 4px を平均化して 1px に潰していくのを繰り返すだけではうまく行きません。 というのも、色んな方向を向いた法線ベクトルの平均は基本的に単位ベクトルではないもっと短いベクトルになってしまうからです。 多くの簡易的な実装では、平均化した後に正規化を行うことで単位ベクトルに戻しています。

しかし、これでは本来はこのレンダリング時にスクリーン空間で 1px に収まる領域（ray の footprint 領域と呼ぶことがある）内に色々な法線方向を含んでいたのに、1 つの特定の方向の法線のみでシェーディングすることになってしまいます。 これでは特に遠くの方などのミップレベルの大きい、より多く縮小されたテクスチャを使う領域で、本来の法線のバリエーションが失われたことによるアーティファクトが発生します。

この図では、この論文のテクニックのアンチエリアスの ON と OFF の比較が示されています。

OFF の場合奥の方のスペキュラのピークを取り逃がしていることが分かります。 本来は色々な方向の法線が含まれる結果として、スペキュラのピークが拾えるはずですが、1px あたり 1 つの法線方向のみをサンプルする通常のリアルタイムシェーディングでは、スペキュラのピークの取り逃がしやちょっとカメラが動くことでそのスペキュラがちらついて見えるなどと言ったアーティファクトが発生します。

この paper では Blinn-Phong モデルの Shininess と強度を下げることで法線の平均長が短いところをラフにする、ということを行っています。

この paper は、のちのちのリアルタイムレンダリングにおけるスペキュラアンチエイリアスの元になっているような技術ということになるのかなと思います。

具体的な手法

この paper では 2 段階に分かれた手法になっています。

1. 最初は法線の平均の長さから法線の分散を計算する。
2. 法線の分散から Blinn-Phong モデルの Shininess と強度を調整する。

Blinn-Phong モデルを前提にしているあたり、時代を感じますね。

法線の分散の計算

法線の分散と言ったときにどのような分散を計算しているかが重要になります。

この paper では、平均法線の方向からの各法線の角度αについてガウス分布を仮定して、その角度の分散σ^2 を計算しています。 角度αがガウス分布に従うという仮定を置いていることになります。

後年のスペキュラアンチエイリアスを扱った論文としては「Stable Geometric Specular Antialiasing with Projected-Space NDF Filtering」のようなものがあります。 こちらの論文では vMF 分布という球面上の分布を使って法線分布関数の分散を扱っています。 それらとは少し異なる手法ですね。

この Toksvig の手法は、角度に関する 1 次元の確率分布で定義域が-∞から∞の分布を扱っていることになり、球面分布のような球面上で積分すると 1 になるような分布になっていないとか、いろいろ理論的には適当な気がします。 とはいえ、vMF 分布をわざわざ持ち出さなくてもそれっぽく軽量に計算できるし、Blinn-Phong モデルの Shininess と強度の調整に使うだけなので、当時の理論としては実用上は十分問題ないということなのでしょう。

この角度についてのガウス分布を実際に計算してみると平均長がどのくらいのときにガウス分布の分散がどうなるかというのが計算できます。

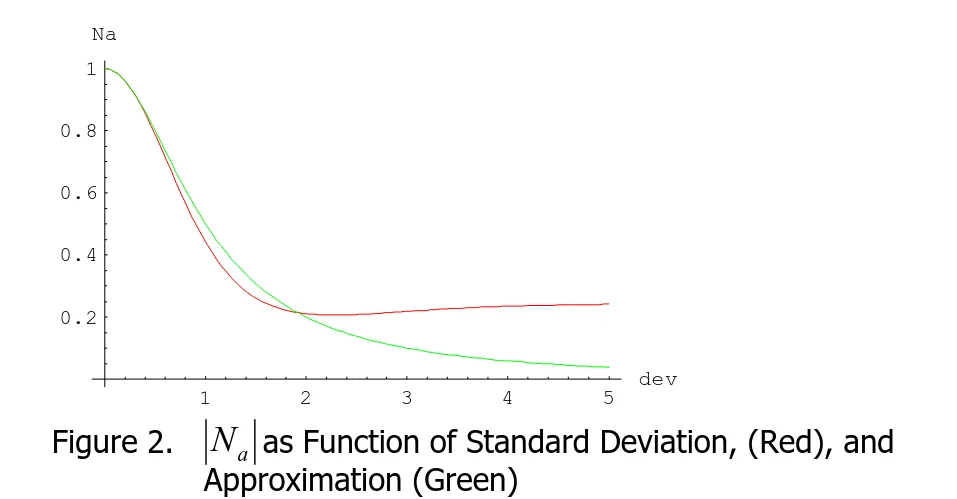
ただしこれは問題があって、ガウスの分散をどれだけ上げても平均長がちゃんと 0 になってくれないようです。 どんだけ分散を上げても、完全にバラバラな方向を向いた法線の平均を取った場合というのは表現できなくて、分散が大きくてもある程度方向を持った平均法線しか扱えないようです。

これを簡易的な数式で近似することで、次の式で平均法線長から分散を計算するようです。

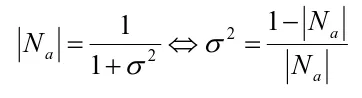
これによって平均長が 0 に近づくようなそれでいて近似としてもまあまあで計算負荷の低い式が得られたということのようです。

だいぶ大雑把で適当なもののような気がします。 ここらへんはやはり後年の vMF 分布を入れたものの方が理論的にきれいに出てくる気がします。

Shininess と強度の調整

Blinn-Phong モデルの Shininess はスペキュラの鋭さを決定するパラメータです。 これをスペキュラのローブの角度についてのガウス分布によるものと仮定して先程の法線平均長から計算されたガウス分布と同じ空間でのガウス分布だと考えることにします。

Blinn-Phong モデルのスペキュラのローブは $\cos^s \alpha$ で表されます。 これを次のようなガウス分布の形で近似します。

これによって $\frac{1}{s}$ がこの Blinn-Phong のガウス分布での分散に対応することになります。

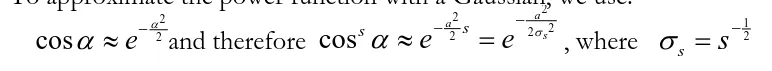
この近似は大体この図のような感じでフィッティングしているようです。

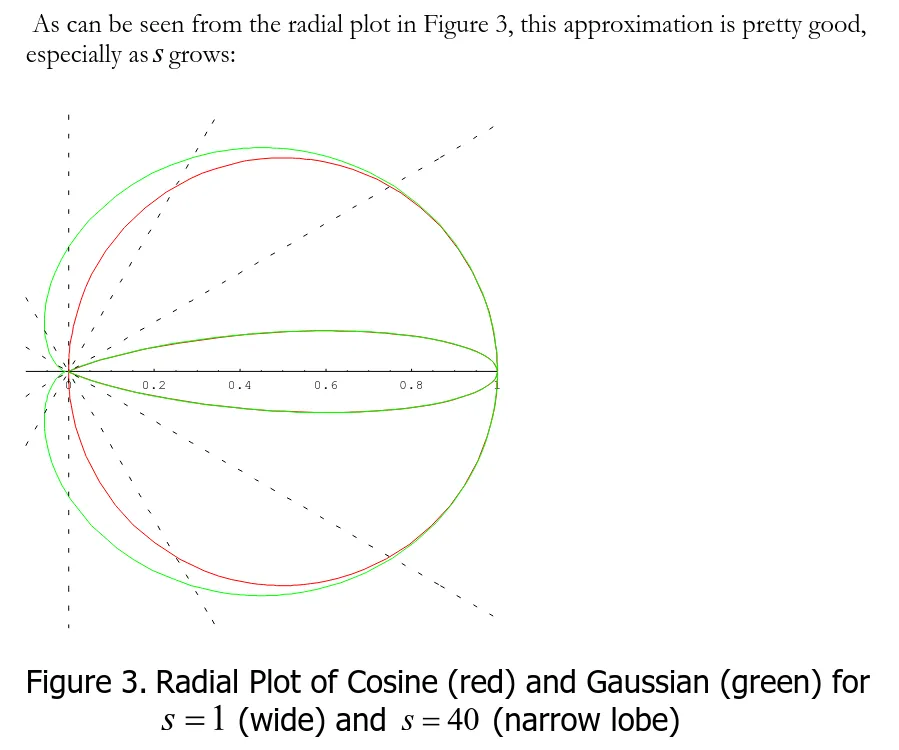
そしてここでガウス分布同士の畳み込みもまたガウス分布になり、その分散は２つの分散の和になるという事実を使います。 Blinn-Phong の Shininess に平均法線長からの分散を畳み込むという形で新しい Shininess が計算できます。 なかなか頭がよいですね。

あとはここから計算を進めれば元の Shininess に footprint 内の法線の分散を畳み込んで調整された Shininess s’が次のように得られます。

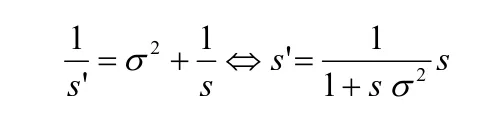
そしてこのままではエネルギー保存が壊れるので、エネルギーの調整のためのファクターも用意する、という形になっています。 半球での積分の値を一定にするという要請から、スペキュラのローブの広がりに対する打ち消しのための係数を加えます。

Blinn-Phong ローブの半球積分は次のような比例の関係です。

スケール係数は次のようになります。

これで最終的には正規化された平均法線を次のように表したとして。

最終的な Toksvig 補正の Blinn-Phong シェーディングは次のようになります。

paper はちょっと式の文字が違いますが$f_t s$が$s'$に対応します。

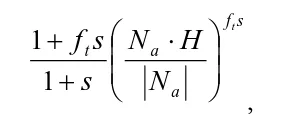
Free Gloss Maps

Free Gloss Maps というのも提案しています。 これがハックしてる手法でなかなか面白いですね。

この手法では法線の平均長を元に粗さを変更していました。 これを利用してテクスチャのマップ数を減らすテクニックだそうです。

Blinn-Phong モデルでは Shininess を材質の粗さごとに持つ必要がありました。 それを、法線マップに正規化されていない長さが短い法線を入れることで、別に Shininess Map を持たなくても法線マップだけで粗さを表現できるようにする、という手法です。

PBR 的な手法とは全く違いますが視覚的なトリックとして面白いことを考えるなあと思いました。

感想

Blinn-Phong 専用の導出ですが、思想は汎用的なもののように思いました。 後年の vMF 分布とか slope space とかでのスペキュラアンチエイリアシングの手法につながる当時としてはよくできたアイデアだったのだろうなと思います。

後年の GGX などの法線分布関数 NDF でラフネスを明示的に持つモデルと違い、Blinn-Phong モデルの Shininess を前提に置いているので、なかなか時代を感じる手法ですが発想自体は現代的なスペキュラアンチエイリアスにもつながるものがこの当時からあったのだなあと思いました。

今回はスペキュラアンチエイリアスの初期の手法として歴史を追いかける意味で目を通してみました。 また後で、後年のスペキュラアンチエイリアスの手法も読み直したいですね。